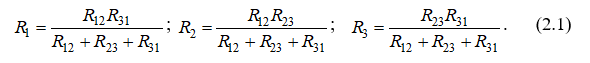Теория / 2.4. Преобразование треугольника сопротивлений в эквивалентную звезду
В некоторых случаях в электрических цепях существуют такие соединения элементов, которые не поддаются расчетам по методу свертывания, так как не содержат ни последовательно, ни параллельно соединенных элементов. Примером такой схемы может служить мостовая схема (рис. 2.8).
Для того чтобы найти эквивалентное сопротивление такой схемы, применяют преобразование треугольника сопротивлений в эквивалентную звезду.
Треугольником сопротивлений называют такое соединение трех элементов, при котором они образуют замкнутый контур, причем между каждой парой элементов имеется узел (рис. 2.9).
Трехлучевой звездой сопротивлений называют такое соединение элементов, при котором одним концом они подсоединены к одному узлу, а другие концы соединяются с остальной цепью (рис. 2.10).
Заменим схему треугольника сопротивлений схемой трехлучевой звезды (рис. 2.11). Обозначим сопротивления звезды R1, R2, R3, а сопротивления треугольника R12, R23, R31. Замена треугольника сопротивлений на трехлучевую звезду будет эквивалентной при условии, что такая замена не изменяет потенциалов узловых точек 1, 2, 3, являющихся вершинами треугольника и концами лучей звезды. Кроме того, такая замена не должна влиять на режим работы остальной части цепи, то есть токи, напряжения и мощности в остальной цепи остаются неизменными.
Общее сопротивление между этими точками определится как
В схеме звезды между этими точками включено сопротивление R3 + R2.
По условию эквивалентности токи I2 и I3 в обеих схемах равны, напряжения между точками 2 и 3 равны, следовательно, должны быть равны и сопротивления, то есть выполняться равенство
Решая совместно эти три уравнения, получим выражения, связывающие сопротивления трехлучевой звезды с сопротивлениями треугольника
Следовательно, треугольник сопротивлений R12, R23, R31 можно заменить трехлучевой звездой с сопротивлениями R1, R2, R3.
В некоторых случаях удобнее для расчетов выполнить преобразование звезды в треугольник. Чтобы рассчитать сопротивления сторон треугольника, зная сопротивления лучей звезды, будем исходить из формул (2.1).
Разделим третье уравнение на первое, получим
Из этих выражение выразим сопротивления R23 и R31 через R12:
Подставим эти выражения в первое уравнение:
Чаще при преобразовании звезды в треугольник пересчитывают не сопротивления, а проводимости ветвей, пользуясь формулами: